Шкала перевода баллов в оценки
Рекомендации по использованию и интерпретации результатов выполнения экзаменационных работ для проведения ОГЭ в 2018 г. (pdf) по предметам.
Шкала пересчета первичного балла за выполнение экзаменационной работы
в отметку по пятибалльной шкале по математике.
2018 год
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, - 32 балла. Из них - за модуль «Алгебра» - 20 баллов, за модуль «Геометрия» - 12 баллов, за модуль «Реальная математика» - 7 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», - 8 баллов, набранные в сумме за выполнение заданий обоих модулей, при условии, что из них не менее 2 баллов получено по модулю «Геометрия».
Шкала пересчёта суммарного балла за выполнение экзаменационной работы в целом в отметку по математике
0—7 баллов — отметка «2»
8—14 баллов — отметка «3»
15—21 баллов — отметка «4»
22—32 баллов — отметка «5»
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:
- для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
- для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
- для физико-математического профиля: 19 баллов, из них не менее 7 по геометрии.
Каталог заданий
Геометрия на клетчатой бумаге
| Задание | Теория и решение | |||
| 1 | На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найдите длину его средней линии, параллельной стороне АС.
|
Ответ: 5 | ||
| 2 | На клетчатой бумаге с размером клетки 1х1 изображен прямоугольный треугольник. Найдите длину его большего катета.
|
| ||
| 3 | На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину ее средней линии
|
Ответ: 6 | ||
| 4 | На клетчатой бумаге с размером клетки 1х1 отмечены три точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС
|
Ответ: 6 | ||
| 5 | На клетчатой бумаге с размером клетки 1х1 изображен ромб. Найдите длину его большей диагонали.
|
| ||
| 6 |
|
| ||
| 7 |
|
|
Статистика и теория вероятностей
Статистические характеристики
Медианой ряда, состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить. Медианой ряда, состоящего из четного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда.
Упорядочить ряд – это значит расположить числа в порядке возрастания.
Среднее арифметическое ряда чисел – это частное от деления суммы этих чисел на число слагаемых
Мода ряда – число, наиболее часто встречающееся в данном ряду.
Размах ряда – разность между наибольшим и наименьшим из чисел
Задачи:
1. Записан рост (в сантиметрах) пяти учащихся: 159, 125, 144, 130, 122. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
Решение: Запишем числа в порядке возрастания: 122, 125, 130, 144, 159. Медиана ряда равна 130.
Среднее арифметическое равно (122+125+130+144+159) : 5 = 136.
Разница между медианой и средним арифметическим: 136 -130 = 6
Ответ: 6
Теория вероятностей
Р- вероятность, А – событие 
0 <Р(А)<1.
Вероятность всегда меньше 1, если событие равновозможное;
равно 1, если событие достоверное;
равно 0, если событие невозможное.
Сумма противоположных событий равна 1: Р(А) + Р(Ã) = 1
Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий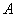 
и 
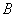равна произведению вероятностей этих событий: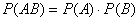 
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий 
или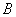 
(без разницы какого), равна сумме вероятностей этих событий: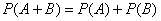 
Задачи:
1. На экзамене 20 билетов, Михаил не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.
Решение: Число благоприятных исходов (выученных билетов): 20 – 4 = 16.
Число всех исходов (всех билетов): 20. Вероятность Р(А) =16:20 = 0,8
Ответ: 0,8
2. Маша выбирает трехзначное число. Найдите вероятность того, что оно делится на 25.
Решени: Всего 900 трехзначных чисел, то есть всех исходов. Из них 900:25 = 36 чисел делятся на 25.
Р(А) = 36 : 900 = 0,04
Ответ: 0,04
3. На тарелке 15 пирожков: 5 с мясом, 4 с капустой и 6 с вишней. Оля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение: Число благоприятных исходов (пирожков с вишней): 6
Число всех исходов (всех пирожков): 15
Р(А) = 6 : 15 = 0,4
Ответ: 0,4
4. В среднем из каждых 50 поступивших в продажу аккумуляторов 46 аккумулятора заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.
Решение: Число благоприятных исходов (аккумулятор не заряжен): 50 – 46 = 4
Число всех исходов (всех аккумуляторов): 50
Р(А) = 4 : 50 = 0,08
Ответ: 0,08
5. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A? (Источник: ГИА-2012. Математика. Диагностическая работа № 2(1вар))
Решение: Каждая команда попадет в группу с вероятностью 4 : 16 = 0,25.
Вероятность того, что команда не попадает в группу равна 1-0,25=0,75.
Ответ: 0,75
6. Определите вероятность того, что при бросании игрального кубика выпадет более 3 очков.
Решение: Число благоприятных исходов (число очков более 3): 4,5,6 – 3 числа
Число всех исходов (всех очков): 6
Р(А) = 3 : 6 = 0,5
Ответ: 0,5
7. Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние 2 раза промахнулся.
Решение: Вероятность попадания в мишень при одном выстреле равна 0,9. Вероятность промаха при одном выстреле равна 1 – 0,9 = 0,1. Так как 3 выстрела – это совместное появление независимых событий, то вероятности умножаются:
0,9·0,1·0,1 = 0,009
Ответ: 0,009
8. В каждом двадцать пятом пакете сока согласно условиям акции под крышкой есть приз. Вера покупает пакет сока. Найдите вероятность того, что Вера не найдёт приз в своём пакете.
Решение:
1 способ. Число благоприятных исходов (пакет сока без выигрыша): 25-1 = 24
Число всех исходов (всех пакетов сока): 25
Р(А) = 24 : 25 = 0,96
2 способ. Вероятность появления приза 1 : 25 = 0,04. Вероятность, что приз не окажется в пакете сока 1 – 0,04 = 0,96
Ответ: 0,96
9. Вероятность того, что новая шариковая ручка пишет плохо(или не пишет) равна 0,13. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Решение: вероятность того, что ручка пишет хорошо равна 1- 0,13 = 0,87
Ответ: 0,87
Окружность, круг и их элементы
Центральные и вписанные углы
